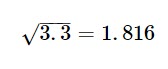مقدمه

تجزیه‌ و تحلیل آماری به معنای بررسی روندها، الگوها و روابط با استفاده از داده‌های کمی است. نتایج حاصل از تجزیه‌ و تحلیل آماری زمانی معتبرند که مطابق با اهداف و سؤالات و فرضیه‌های تحقیق، طراحی مطالعه، حجم نمونه و روش نمونه‌گیری به‌طور صحیح انتخاب و اجرا شده باشد. آمار به ما کمک می‌کند تا داده‌های کمی را برای کمک به تصمیم‌گیری به اطلاعات مفیدی تبدیل کنیم. 

دو حوزه مهم در آمار عبارتند از آمار توصیفی و استنباطی. 

آمار توصیفی 

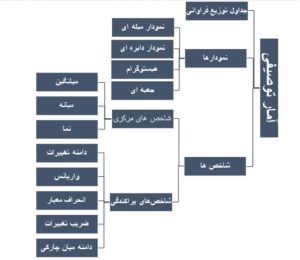
از آمار توصیفی (descriptive statistics) برای سازمان‌دهی، خلاصه‌سازی و نیز توصیف داده‌ها و الگوها استفاده می‌شود. ابزارهای آمار توصیفی شامل نمودارها، جداول توزیع فراوانی و شاخص‌ها است که در شکل زیر ارائه شده است. 

جدول توزیع فراوانی

در آمار، فراوانی به تعداد دفعاتی گفته می شود که یک ویژگی یا داده تکرار شود. به‌ عنوان مثال، اگر چهار دانش‌آموز دارای نمره 15 در ریاضیات باشند؛ لذا فراوانی نمره 15 برابر با 4 است یا اگر از بین 100 نوزاد متولدشده، 2 نوزاد دارای رنگ چشم آبی باشند، فراوانی رنگ چشم آبی در نوزادان برابر با 2 می باشد. جدول توزیع فراوانی (frequency table) نیز جدولی است که به‌وسیله آن فراوانی و یا به عبارتی تعداد تکرار وقوع یک خصوصیت یا داده نمایش داده می‌شود. این جدول شامل چند سطر و ستون است. در سطرها مقادیر متغیر کیفی یا حدود طبقات متغیر کمی موردنظر لیست می‌شوند و در ستون‌ها، انواع فراوانی‌ شامل فراوانی مطلق، فراوانی نسبی، فراوانی تجمعی و فراوانی تجمعی نسبی مربوط به هر سطر ثبت می‌شوند. 

فراوانی مطلق 

از شمارش تعداد دفعاتی هر طبقه تکرار می‌شود، به دست می‌آید و با f نمایش داده می‌شود. مجموع تعداد فراوانی‌های مطلق (absolute frequency) برابر با تعداد کل مشاهدات است. 

فراوانی نسبی

فراوانی نسبی (relative frequency) از تقسیم فراوانی‌های مطلق هر طبقه بر تعداد کل مشاهدات به دست می‌آید و با r نمایش داده می‌شود. می‌توان مقدار آن را به‌صورت درصد نیز نمایش داد. برای این کار کافی است آن را در ۱۰۰ ضرب کنیم و حاصل را با علامت ٪ نشان دهیم. مجموع تعداد فراوانی‌های نسبی برابر با یک و در صورت بیان شدن به درصد برابر با 100 است. 

فراوانی تجمعی

 منظور از فراوانی تجمعی (cumulative frequency) هر طبقه، مجموع فراوانی‌های مطلق آن طبقه و طبقات ماقبل آن است و با F نمایش داده می‌شود. فراوانی تجمعی آخرین طبقه برابر با تعداد کل مشاهدات است. 

فراوانی تجمعی نسبی

 منظور از فراوانی تجمعی نسبی (cumulative relative frequency) هر طبقه، مجموع فراوانی‌های نسبی آن طبقه و طبقات ماقبل آن است. فراوانی نسبی آخرین طبقه برابر با یک و در صورت بیان شدن به درصد برابر با 100 است. 

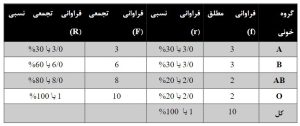
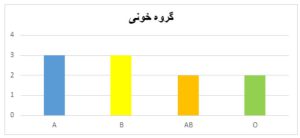
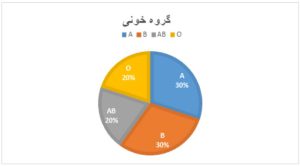
مثال 1- جدول فراوانی متغیر کیفی  

گروه خون برای ۱۰ نفر از دانشجویان به‌صورت AB,A,A,B,B,AB,B,O,A,O ثبت شده است. جدول فراوانی برای این افراد بر اساس گروه خون به‌صورت زیر است. 

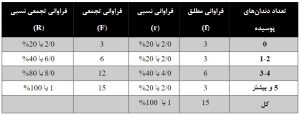
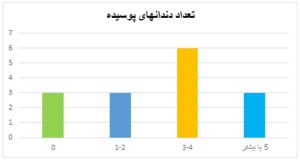
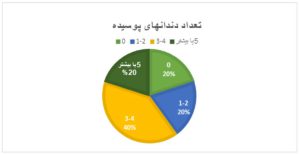
مثال 2- جدول فراوانی متغیر کمی  

تعداد دندان‌های پوسیده 15 دانش‌آموز به‌صورت 0،1، 2،4،6،5،2،1،0،0،3 ، 3، 2، 4، 5 ثبت شده است. جدول فراوانی برای این افراد بر اساس تعداد دندان‌های پوسیده به‌صورت زیر است. 

نمودارهای آماری 

نمودار (گراف، پلات یا چارت) ابزاری است که برای توصیف و نمایش تصویری داده‌های جمع‌آوری‌ شده به‌کار برده می‌شود. از مزیت‌های نمودارهای آماری این است که به پژوهشگر کمک می‌کند تا ویژگی‌های داده‌ها را بهتر و آسان‌تر توصیف کند و مخاطب قادر خواهد بود اطلاعات حاصل از آن‌ را سریعتر درک کند. نمودارهای مختلفی در آمار وجود دارد که متداول‌ترین آن‌ها عبارت‌اند از: 

نمودار میله‌ای یا ستونی 

 در نمودار میله ای (bar chart) دو محور عمود بر هم وجود دارد. محور افقی نشان‌دهنده نام رده‌ها یا طبقات و محور عمودی نشان‌دهنده فراوانی داده‌ها (فراوانی مطلق یا نسبی) است. برای هر طبقه، میله‌ای به ارتفاع فراوانی آن طبقه رسم می‌شود. این نمودار معمولاً برای نمایش توزیع فراوانی متغیرهای کیفی یا کمی گسسته به کار می‌رود.

نمودار دایره‌ای 

 نمودار دایره ای (pie chart) به شکل یک دایره است که به قطاع‌هایی تقسیم شده است. تعداد قطاع‌ها برابر با تعداد رده‌ها یا طبقات است. اندازه هر قطاع از دایره، بیانگر درصد فراوانی آن گروه است و از ضرب فراوانی نسبی در 360 به دست می‌آید. این نمودار معمولاً برای نمایش توزیع فراوانی متغیرهای کیفی یا کمی گسسته با تعداد سطوح کم استفاده می‌رود.

نمودار مستطیلی یا هیستوگرام

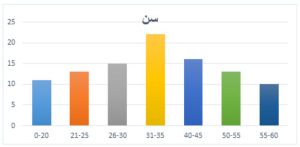
نمودار هیستوگرام (histogram) برای نمایش متغیرهای کمی پیوسته (مقیاس فاصله‌ای یا نسبتی) به کار می‌رود و شبیه نمودار میله‌ای است با این تفاوت که در هیستوگرام ستون‌ها به یکدیگر چسبیده‌اند. در هیستوگرام هر مستطیل نشان‌دهنده یک طبقه است که عرض آن برابر حدود آن طبقه و ارتفاع آن مساوی فراوانی همان طبقه است. از اتصال نقاط وسط مستطیل‌ها به یکدیگر و اتصال ابتدا و انتهای آن به نقطه وسط یک طبقه فرضی به ترتیب قبل و بعد از اولین و آخرین طبقه، نمودار چندبر فراوانی به‌دست می‌آید که از روی آن می‌توان از شکل توزیع (نرمال بودن، وضعیت چولگی و کشیدگی) متغیر مدنظر اطلاع پیدا کرد. نمودار هیستوگرام زیر مربوط به سن 100 نفر است. 

نمودار جعبه‌ای

نمودار جعبه ای (box plot) به كمك شاخص‌های مركزي و پراكندگی، توزیع داده‌ها را به شكلي بسيار گويا و مفيد ارائه می‌دهد. با استفاده از اين نمودار می‌توان مركزيت،‌ پراكندگي و چولگي داده‌ها را تفسير نمود. نمودار جعبه‌ای از یک جعبه و دو میله که از آن بیرون آمده تشکیل شده است. طول جعبه برابر است با فاصله بین چارک اول و سوم. در داخل جعبه، یک خط افقی دیده می شود که موقعیت میانه نمایش می دهد. لذا نمودار جعبه‌ای اطلاعاتی راجع به گرایش مرکزی و تغییرپذیری 50 درصد میانی توزیع را فراهم می‌کند. دو انتهای بالا و پایین جعبه با میله‌ای به مقادیر ماکزیمم و می نیمم متصل می‌شود. داده های پرت (در صورت وجود) که مقادیر بالاتر از 3 برابر دامنه میان چارکی دارند، با علامتی مانند E و مقادیر با حداقل پرت شدگی (در صورت وجود) ) که بین 5/1 برابر دامنه میان چارکی و 3 برابر دامنه میان چارکی هستند در دو طرف جعبه با علامتی مثل O در دو انتهای بالا و پایین جعبه نمایش داده می‌شوند.  

شاخص‌های عددی 

شاخص‌های عددی برای توصیف داده‌ها شامل شاخص‌های مرکزی و پراکندگی هستند.

شاخص‌های مرکزی

شاخص‌های مرکزی (central indeces) کمیت‌های توصیفی هستند که محل تمرکز و یا تجمیع داده‌ها را نشان می‌دهند. رایج‌ترین شاخص‌های مرکزی شامل میانگین، میانه و نما هستند. 

میانگین

شناخته‌شده‌ترین و متداول‌ترین مقدار متوسطی است که مورد استفاده قرار می‌گیرد، میانگین (mean یا average) می باشد. انواع مختلفی مانند میانگین حسابی، هندسی و هارمونیک را دارد که میانگین حسابی به‌مراتب رایج‌تر است. از مزیت‌های میانگین حسابی این است که (1) محاسبه آن آسان است، (2) از تمامی داده‌ها در محاسبه آن استفاده می‌شود، (3) یکتاست و برای یک مجموعه داده فقط یک مقدار مشخص دارد. از معایب این شاخص این است که تحت تأثیر داده‌های پرت است و در این حالت یک شاخص مرکزی گمراه‌کننده است. این شاخص از مجموع تمام مشاهدات تقسیم بر تعداد داده‌ها به دست می‌آید. به‌طور مثال، اگر مقادیر مدت بستری 5 زن سالمند برابر با 12، 7، 9، 10 و 10 ساعت باشد میانگین حسابی برابر است با: 

10+10+9+7+12=48÷5=6/9 

میانه

 میانه (median) داده‌ای است که اگر آن‌ها را از کوچک به بزرگ مرتب کنیم، در وسط داده‌ها قرار می‌گیرد. درصورتی‌که تعداد داده‌ها فرد باشد داده وسط و اگر تعداد داده‌ها زوج باشد، میانگین دو داده‌‌ی وسط به‌عنوان میانه گزارش می‌شود. از مزایای این شاخص این است که یکتاست و تحت تأثیر داده‌های پرت قرار نمی‌گیرد. از معایب این شاخص نیز این است که در محاسبه آن از همه داده‌ها استفاده نمی‌شود. . به‌طور مثال، اگر مقادیر مدت بستری 5 زن سالمند برابر با 12، 7، 9، 10 و 10 ساعت باشد میانه برابر است با داده وسط در داده‌های مرتب‌شده یعنی 10. 

نما 

نما یا مد (mode) عبارت است از داده‌ای که بیشترین فراوانی را در بین داده‌ها دارد. به‌طور مثال، اگر مقادیر مدت بستری 5 زن سالمند برابر با 12، 7، 9، 10 و 10 ساعت باشد نما برابر است با 10. از مزایای این شاخص سادگی محاسبه آن و از معایب آن عدم یکتایی است. به این معنا که اگر چندین داده به‌طور یکسان دارای بیشترین فراوانی باشند، همه آن داده‌ها به‌عنوان نما گزارش می‌شوند.  

شاخص‌های پراکندگی 

شاخص‌های پراکندگی (dispersion indexes) کمیت‌های توصیفی هستند که میزان پراکندگی داده‌ها را نسبت به محل تمرکز و یا تجمیع داده‌ها نشان می‌دهند. رایج‌ترین شاخص‌های پراکندگی شامل دامنه تغییرات، واریانس، انحراف معیار، ضریب تغییرات و دامنه‌ی میان چارکی هستند. 

دامنه تغییرات 

دامنه تغییرات (range) ساده‌ترین شاخص پراکندگی است که از تفاوت کمترین و بیشترین مقدار یک متغیر به دست می‌آید.  

به‌طور مثال، اگر مقادیر مدت بستری 5 زن سالمند برابر با 12، 7، 9، 10 و 10 ساعت باشد دامنه تغییرات آن برابر است با 

7-12=5  

از مزایای این شاخص سادگی محاسبه آن و از معایب آن این است که تنها دو داده‌ی ابتدایی و انتهایی در محاسبه آن شرکت می‌کنند و سایر داده‌ها نقشی ندارند. 

واریانس

واریانس (variance) یکی از شاخص‌های پراکندگی است که از مجموع مجذور انحرافات داده‌ها از میانگین تقسیم بر 1-n به دست می‌آید (n تعداد داده‌هاست).  

به‌طور مثال، اگر مقادیر مدت بستری 5 زن سالمند برابر با 12، 7، 9، 10 و 10 ساعت باشد واریانس آن برابر است با 

10+10+9+7+12=48÷5=6/9 میانگین

2(6/9-10)+2(6/9-10)+2(6/9-9)+2(6/9-7)+2(6/9-12)= 3/3 میانگین

از مزایای آن این است که در محاسبه‌ی آن از همه‌ی داده‌ها استفاده می‌شود و از معایب آن این است که در صورت وجود داده‌های پرت در داده‌ها شاخص پراکندگی مناسبی نیست. 

انحراف معیار 

از جذر واریانس، انحراف معیار (standard deviation) به دست می‌آید.  

به‌طور مثال، انحراف معیار داده‌های مدت بستری 5 زن سالمند برابر است با 

از مزایای این شاخصه آن است که برخلاف واریانس، واحد آن با واحد اندازه‌گیری داده‌ها یکسان است.  

ضریب تغییرات 

از تقسیم انحراف معیار بر میانگین، ضریب تغییرات (coefficient of variation) به دست می‌آید و معمولاً به‌صورت درصد بیان می‌شود. برای مقایسه‌ی پراکندگی دو متغیر که واحد اندازه‌گیری متفاوت دارند یا یک متغیر در دو جامعه‌ی متفاوت مناسب است. هرچه ضریب تغییرات کمتر باشد، پراکندگی آن متغیر حول میانگین کمتر است. 

به‌طور مثال، انحراف معیار داده‌های مدت بستری 5 زن سالمند برابر است با  

816/1÷6/9=189/0

×

100= 9/18      

دامنه میان چارکی   

دامنه میان چارکی (interquartile range) یکی از شاخص‌های پراکندگی است که از تفاضل چارک اول و سوم به دست می‌آید. چارک اول عددی است که 25 درصد داده‌ها کوچک‌تر یا مساوی آن هستند و چارک سوم عددی است که 75 درصد داده‌ها کوچک‌تر یا مساوی آن هستند.  

سه نوع چارک وجود دارد. چارک دوم همان میانه است یعنی نیمی از داده‌ها از آن کوچک‌تر و نیمی از داده‌ها از آن بزرگ‌تر هستند. وقتی تعداد داده‌ها فرد باشد، دقیقا داده‌ی وسطی پس از مرتب کردن از کوچک به بزرگ، چارک دوم خواهد بود. زمانی که تعداد داده‌ها زوج است، چارک دوم برابر با میانگین دو داده‌ی وسطی پس از مرتب‌سازی می باشد. اکنون چارک اول میانه‌ی داده‌های اول تا قبل از خود میانه (پس از مرتب‌سازی) و چارک سوم میانه‌ی داده‌های بعد از میانه تا آخر (پس از مرتب‌سازی) است. 

به‌طور مثال، دامنه‌ی میان چارکی داده‌های 2,5,6,8,11,12,13,17,18,79,1022 برابر است با 

۱۱ داده داریم، پس داده‌ی ششم، میانه است. خوشبختانه داده‌ها مرتب‌شده هستند. پس میانه (چارک دوم) برابر است با ۱۲  

اکنون داده‌های پیش از میانه برابر هستند با؛ 2,5,6,8,11 

تعداد آن‌ها ۵ است، پس میانه‌اش (که چارک اول کل داده‌های پرسش اصلی است) داده‌ی سوم یعنی ۶ می‌شود. 

داده‌های پس از میانه برابر هستند با؛ 

13,17,18,79,1022 

تعداد ۵ داده بعد از میانه‌ (چارک سوم کل داده‌های پرسش اصلی) قرار دارند. بنابراین، داده‌ی سوم، عدد ۱۸، برابر با چارک سوم خواهد بود. 

لذا دامنه‌ی میان چارکی داده‌ها برابر است با:   

12-18=6  

آمار استنباطی 

به مجموعه روش‌هایی که به استنباط در مورد ویژگی‌های ناشناخته‌ی جامعه می‌انجامد، آمار استنباطی (inferential statistics) گفته می‌شود. هدف از آمار استنباطی آن است که با انتخاب و بررسی بخشی از جامعه به‌عنوان نمونه که خصوصیات جامعه را در برداشته باشد در مورد ویژگی‌های ناشناخته‌ی جامعه‌ مانند میانگین و نسبت یا واریانس (پارامترهای جامعه)، برآورد یا «استنباط» صورت گیرد، به‌عبارت‌دیگر در آمار استنباطی، نتایج حاصل از نمونه به جامعه تعمیم (generalize) داده می‌شود. 

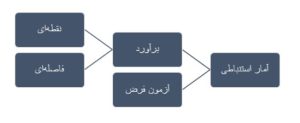
استنباط آماری به‌طورکلی به 2 بخش تقسیم می‌شود: برآورد و آزمون فرضیه 

برآورد

برآورد (estimation) به معنای تخمین زدن است. در آمار دو نوع برآورد داریم: برآورد نقطه‌ای و برآورد فاصله‌ای 

برآورد نقطه‌ای

در برآورد نقطه‌ای (point estimation)، یک پارامتر با مقدار مجهول را براساس یک عدد واحد که از داده‌های نمونه محاسبه می‌شود، تخمین می‌زنیم.  

به‌عنوان مثال، متوسط (میانگین) دستمزد ماهانه کارمندان یک اداره بر اساس نمونه‌ای 20 تایی از بین کل کارمندان، 5500000 تومان است. درواقع میانگین دستمزد نمونه‌ی انتخابی به‌عنوان تخمینی برای میانگین دستمزد کل کارمندان اداره استفاده می‌شود. 

برآورد فاصله‌ای یا فاصله اطمینان 

در برآورد فاصله‌ای (confidence interval)، محدوده‌ای از مقادیر را می‌یابیم که معتقدیم پارامتر جمعیت واقعی با احتمال زیاد در آن محدوده قرار دارد. برآورد فاصله‌ای برای هر پارامتر بر اساس فرمولی مشخص و علمی به دست می‌آید و محدوده‌ی تعیین‌شده به سطح اطمینان انتخابی بستگی دارد که معمولاً 90% ، 95% یا 99% انتخاب می‌شود. هر چه سطح اطمینان بیشتر شود طول فاصله‌ی به‌دست‌آمده کمتر و دقت بیشتر می‌شود. 

به‌عنوان مثال، متوسط دستمزد ماهانه کارمندان یک اداره بر اساس نمونه‌ای 20 تایی از بین کل کارمندان، با سطح اطمینان 95 درصد بین 5200000 تومان تا 5800000 است.  

آزمون فرض

در آزمون فرض (hypothesis test) باید بر اساس داده‌های نمونه تصمیم بگیریم که آیا گزاره یا ادعایی که در مورد پارامتر جمعیت مطرح شده است درست یا غلط است.  

 به‌عنوان مثال، این ادعا که میانگین دستمزد ماهانه کارمندان یک اداره بیش از 5000،000 تومان است ، می‌تواند با استفاده از داده‌های نمونه مورد آزمون قرار گیرد. 

آزمون فرض یا بررسی فرضیه‌های پژوهش، بر اساس نتایج آمار استنباطی ارائه می‌شود و این هدف از طریق پاسخ به پرسش‌های زیر انجام می‌شود: 

نوع فرضیه چیست؟ رابطه‌ای، مقایسه‌ای یا علی؟ 

نوع متغیر موردبررسی و مقیاس اندازه‌گیری آن چیست؟ 

پارامتر موردبررسی چیست؟ 

تعداد گروه‌های مقایسه شونده چقدر است؟ 

آیا پیش‌فرض آزمون آماری برقرار است یا خیر؟ 

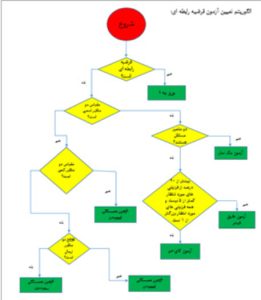
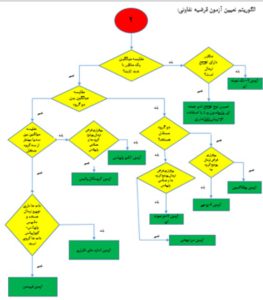
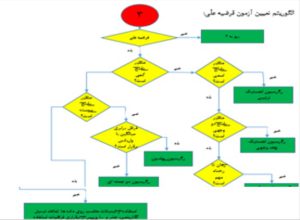
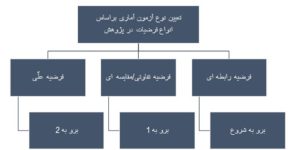
پاسخی که محقق به هر یک از سؤال‌های فوق می‌دهد درواقع، تعیین‌کننده‌ی آزمونی است که او برای تجزیه‌ و تحلیل داده‌ها انتخاب می‌کند. چارت‌های زیر (چارت 1، 2 و 3) به‌منظور شناسایی آزمون‌های مناسب آماری ارائه شده است. 

فرضیه‌ی رابطه‌ای 

همواره در رابطه با دو متغیر به کار می‌رود. محقق در این فرضیه قصد دارد که صرفاً درجه و جهت رابطه‌ی بین متغیرها را کشف کند. این فرضیه به‌صورت جهت‌دار و بدون جهت مطرح می‌شود: 

مثال جهت‌دار: بین تحصیلات و اعتماد اجتماعی رابطه مستقیم وجود دارد. 

مثال بدون جهت: بین تحصیلات و اعتماد اجتماعی رابطه وجود دارد. 

فرضیه‌ی تفاوتی/مقایسه‌ای 

در فرضیه‌ی مقایسه‌ای، به دنبال بررسی و مقایسه‌ی تفاوت اثر دو یا چند متغیر یا گروه بر یک یا چند متغیر دیگر هستیم. در این فرضیه معمولاً درصدد مقایسه‌ی میانگین (آزمون‌های پارامتری) و یا میانه (آزمون‌های ناپارامتری) متغیرها در بین گروه‌ها هستیم مثلاً مقایسه‌ی میانگین یا میانه با یک مقدار ثابت و یا مقایسه بین دو گروه و بیشتر. 

مثال: میزان اعتماد اجتماعی در بین زنان و مردان متفاوت است که درصورتی‌که اعتماد اجتماعی به‌صورت یک متغیر کمی جمع‌آوری شده باشد می‌تواند به‌صورت مقایسه‌ی میانگین نمره‌ی اعتماد اجتماعی بین دو گروه زنان و مردان مطرح شود. 

فرضیه‌ی علی 

هدف فرضیه‌های علی، کشف و تعیین رابطه‌ی علت و معلولی بین دو یا چند متغیر است. محقق در این فرضیه به دنبال این است که بگوید آیا متغیری می‌تواند علت به وجود آمدن متغیر دیگر باشد یا خیر. فرضیه‌های علی می‌توانند به سه حالت مختلف بیان شوند: 

حالت 1: پشتکار، علت پیشرفته است. 

حالت 2: پشتکار، بر پیشرفت مؤثر است. 

حالت 3: پشتکار، یکی از عوامل پیشرفت است.